El problema del ajedrez y el trigo

Hoy vamos a ver cómo resolver el problema de los granos de trigo que pidió el creador del ajedrez, Sessa, al rey de la India.

Cuenta la leyenda que el creador del ajedrez, llamado Sessa, le enseñó su invento al rey de la India. Entonces, el rey quedó tan alucinado que preguntó a Sessa qué recompensa quería por su invento. Él, que era muy sabio, le dijo al rey que quería por la primera casilla, un grano de trigo; por la segunda, dos; por la tercera, cuatro… Y así constantemente, duplicando esa cantidad en cada casilla hasta llegar a la casilla número 64. El rey aceptó, pero no sabía lo que se le venía encima.

A continuación exprimiremos la resolución del problema al máximo.

Resolución rápida del problema del ajedrez y el trigo

Vemos claro que, si por cada casilla, la cantidad se multiplica por dos, bastará con elevar 2 a la cantidad de casillas para conseguir la cantidad de la última casilla: 2^64 ≈ 18,5 trillones de granos de trigo.

Como muchos os habréis dado cuenta, esta potencia no da pie a que la casilla número 1 tenga un grano de arroz, sino 2. Porque todos sabemos que 2^1 = 2 y no a 1. Pero, 2^0 = 1 y no a 2. Pensando un poco podemos deducir que para ello podemos elevar al total de casillas (64) menos una (63) para que la primera (será la 0) tenga un grano de trigo. Ahora sí, 2^63 = 9 223 372 036 854 775 808.

Perfecto, ya tenemos los granos de trigo de la casilla número 64 (o 63 en nuestra potencia). Pero el problema nos pide a mayores lo de las últimas 63 casillas. Menudo papelón pensaréis algunos.

Vamos a pensar un poco. Si comenzamos con las primeras potencias de base 2…

• 2^0 = 1
• 2^1 = 2
• 2^2 = 4
• 2^3 = 8
• 2^4 = 16
• …

Si pensamos, vemos que la suma de todas las potencias de base 2 de, en este caso, exponente de 0 a 4 (1 + 2 + 4 + 8 + 16), es igual a la potencia de base 2 con exponente uno mayor que el mayor de este grupo.

Es decir, 2^0 + 2^1 + … + 2^4 = 1 + 2 + 4 + 8 + 16 = 31. La potencia con mayor exponente de esta suma es 2^4, luego hacemos 2^5 y restamos 1 y se supone que debería dar 31. Probémoslo: 2^5 – 1 = 32 – 1 = 31.

Sabiendo esto podemos deducir que la suma de todas las potencias con base 2 y exponente desde 0 hasta 62 será 2^63 – 1. Así que, calculemos pues:

granosTrigo = 2^63 + (2^63 – 1) = 2^63 * 2 – 1 = 9 223 372 036 854 775 808 * 2 – 1 = 18 446 744 073 709 551 616 – 1 = 18 446 744 073 709 551 615

Entonces, el total de granos de trigo que el rey ha de otorgar a Sessa es de unos 18 trillones y medio aproximadamente.

Pero, ¿cuánto tarda en crecer esto?

En la India según este artículo de swissinfo.ch se producen 107 millones de toneladas de trigo anuales.

Según este estudio, 200 granos de arroz pesan entre 8,42 g y 11,25 g. Tomando como valor la media, es decir, 9,835 g, calculamos que en 1 tonelada hay, aproximadamente, 20 335 000.

Si multiplicamos esta cantidad por los 107 millones de toneladas:

107 000 000 * 20 335 000 = 2,175845 * 10^15 = 2 175 845 000 000 000 granos de trigo

Entonces, ¿cuánto se tardará en la India en producir los 18 trillones y medio de granos de trigo?

Para calcularlo, dividiremos 18,5 (trillones de granos de trigo a producir) entre 0,002175845 (trillones de granos de trigo producidos anualmente):

18,5 / 0,002175845 = 8 502 años.

Es decir, si el rey diera a Sessa toda la producción de granos de trigo de la India, tardaría 8 502 años en cumplir con su recompensa.

Función exponencial de los granos de trigo

Si recordamos la resolución del problema de la entrada anterior, recordaremos que por cada casilla, aumentábamos por uno el exponente de la potencia con base 2, es decir:

• Casilla 1: 2^0 = 1 grano
• Casilla 2: 2^1 = 2 granos
• Casilla 3: 2^2 = 4 granos
• …

Esto lo podemos describir como una función exponencial: f(x) = 2^x

Con ayuda del GeoGebra, la representaremos:

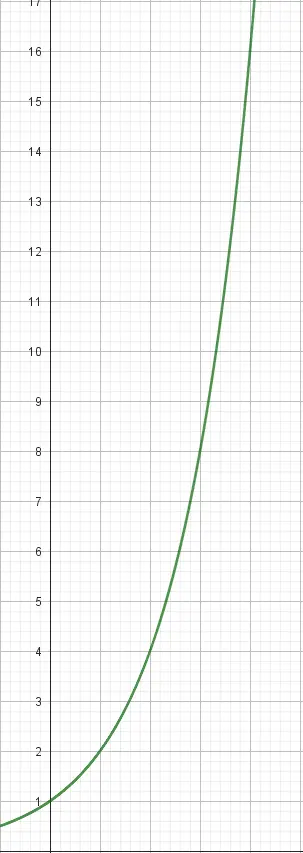
Como podemos observar, cada vez la función crece más rápido, pues esta es la base de un crecimiento exponencial, el cual se ve reflejado en las funciones exponenciales como esta.

Es importante saber lo siguiente, pues tenemos dos opciones: contar la primera casilla como la casilla número 0 y, de esta forma, en la primera casilla, elevar 2 a 0 o elevar 2 a x-1.

¿Por qué esto?

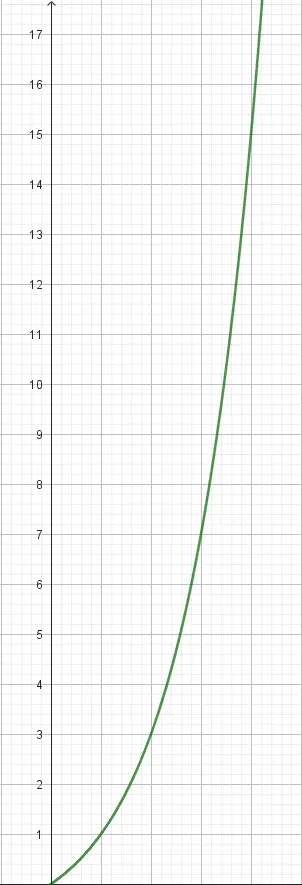
Si elevamos en la primera casilla 2 a 1, 2^1 = 2 granos de trigo y se supone que en la primera casilla solo podemos tener un grano, por lo que, o contamos la primera casilla con el número 0 y la última con el número 63 o elevamos a x (número de casilla) – 1.

En la siguiente imagen vemos la función f(x) = 2 ^ (x-1)

Programa en Python

Para terminar de sacarle jugo a este problema vamos a hacer un pequeño programa en Python para que calcule cuántos granos de arroz habrá en x casilla y cuántos granos de arroz habrá en total hasta x casilla.

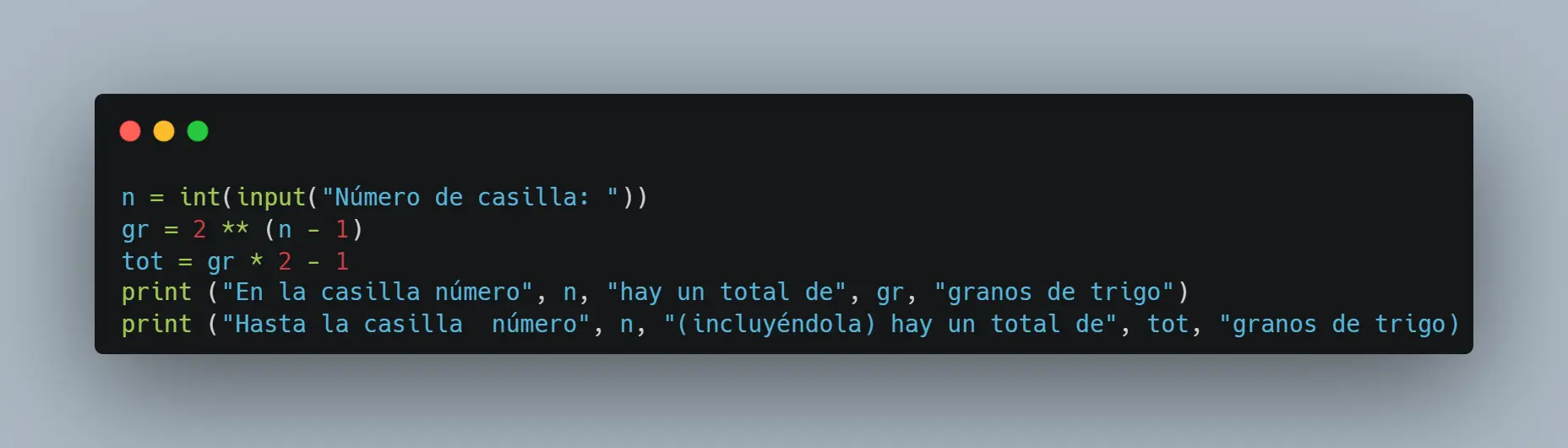
Analicemos línea por línea:

1. La primera línea crea una variable “n” que le asigna el valor entero de la respuesta a la pregunta “Número de casilla: “.

2. La segunda línea crea una variable “gr” que será el número de granos en la casilla n. Se le asigna el siguiente valor: 2 ^ (n – 1). Es el mismo valor que hemos asignado antes a nuestra función, solo que en el programa tenemos que utilizar ** para indicar que es una potencia.

3. La tercera línea crea una variable “tot” que será el número de granos hasta la casilla n incluyéndola. Se le asigna el siguiente valor: gr (número de granos en casilla n) * 2 – 1. En la otra entrada explicamos que la suma de todos los valores de una función exponencial hasta n, es igual que ese número (n) multiplicado por dos menos uno.

4. La cuarta línea imprime (escribe) lo siguiente, para poner el ejemplo, supongamos que hemos asignado el valor 2 a n: “En la casilla número 2 hay un total de 2 granos de trigo.” En otras ocasiones, pondríamos un str() alrededor de n o gr para hacer las variables string en vez de int (integger), pero en esta ocasión, como no las estamos sumando, no es necesario.

5. La quinta línea imprime (escribe) lo siguiente, para poner el ejemplo, supongamos que hemos asignado el valor 2 a n: “Hasta la casilla número 2 (incluyéndola) hay un total de 3 granos de trigo.” Este 2 sería el valor de n y el 3 sería el valor de tot (granos totales hasta n casilla).