Un copo de nieve, tan básico como frío y como rápido se deshace al tocarlo, está lleno de matemáticas, aunque no lo parezca. Hoy nos adentraremos en el corazón de un copo de nieve para explicar las matemáticas que contiene, haremos un programilla de Python para automatizar la parte matemática y una representación interactiva en Geogebra. ¡Vamos allá con las matemáticas de un copo de nieve!
Explicación matemática del copo de nieve
Un copo tiene seis palos largos, cada segmento sobresaliente del cual salen palitos pequeños. Cada palo largo tiene una longitud, a la que llamaremos “l”. Entre cada dos palos pequeños hay una distancia de separación, a la que llamaremos “d”. Sabiendo “l” y sabiendo “d”, sabremos la cantidad de palos pequeños que hay en un copo.
Hay un cálculo con el que podríamos saber los palos pequeños de cada copo. Es la siguiente:
l/d //cantidad de pares de palos pequeños en cada palo largo// * 2 //para saber los palos pequeños en cada palo largo, es decir, multiplicamos los pares por 2 para saber el total// * 6 //para saber los palos pequeños en el copo en total, ya que tiene 6 palos largos//
Pongamos un ejemplo:
- L (longitud): 5
- D (distancia): 1
Entonces, haremos el siguiente cálculo:
5/1·2·6 = 60
Con esos datos, habrá un total de 60 palos pequeños en el copo.
Programa en Python
A continuación, mostraremos el programa de Python con el que se puede calcular automáticamente la cantidad de palos cortos por palo largo, la cantidad total de palos cortos y la posición de ellos relativa a cada palo largo.
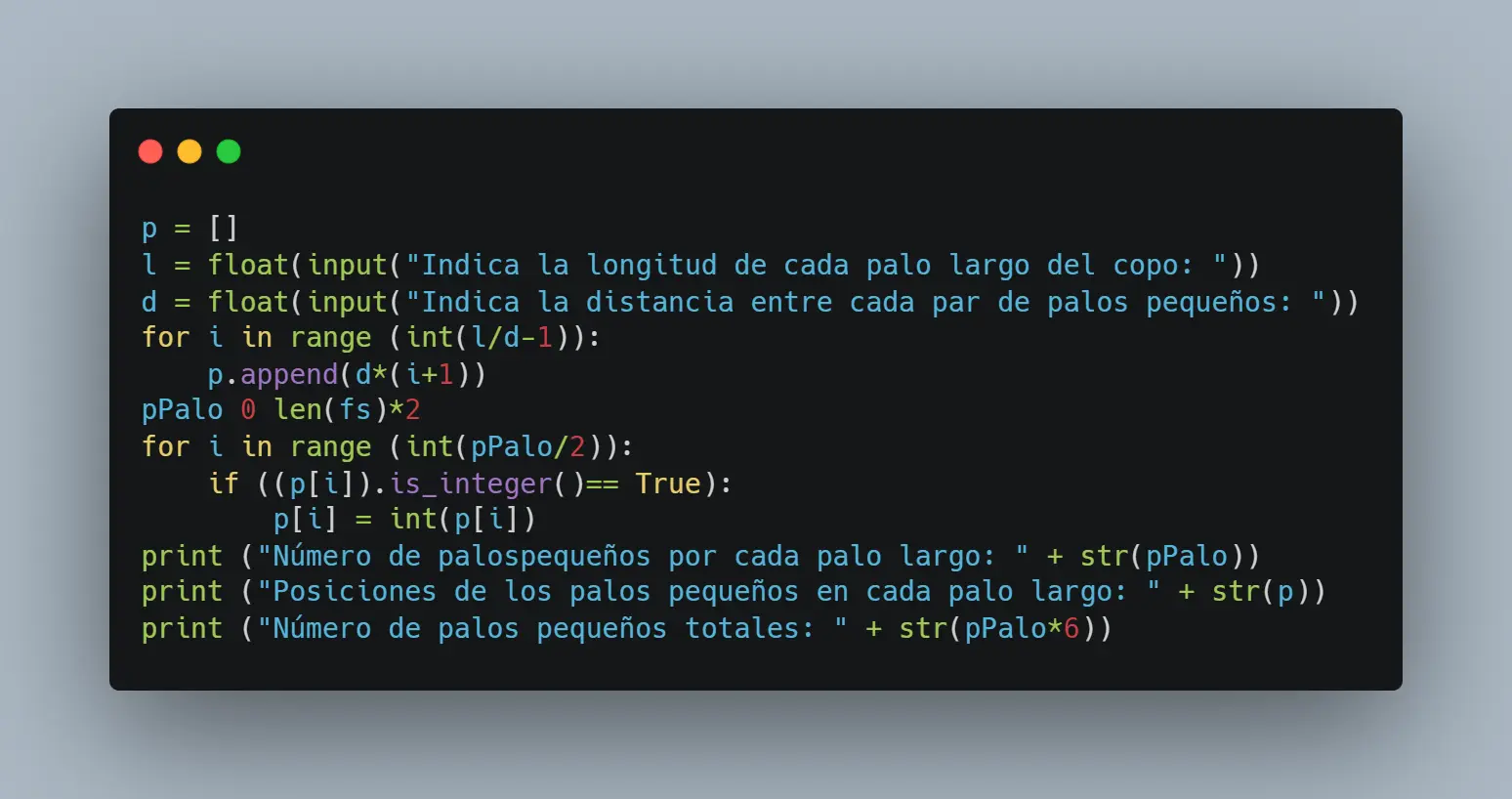
Ese sería el código en Python, y a continuación, una demostración de ello:
Esta es la explicación del código línea por línea:
-
Crea una lista que se llama p, haciendo referencia a los palos pequeños. En ella escribiremos las posiciones de los palos pequeños en cada palo largo. IMPORTANTE: por lo tanto, en esta lista habrá tantos elementos como pares de palos pequeños.
-
Crea una variable llamada l, que hará referencia a la longitud de cada palo largo. El valor de ella será lo que responda la persona a la pregunta: “Indica la longitud de cada palo largo del copo: “.
-
Crea una variable llamada d, que hará referencia a la distancia de separación entre cada par de palos pequeños. El valor de ella será lo que responda la persona a la pregunta: “Indica la distancia entre cada par de palos pequeños: “.
-
Repetirá la línea 5 tantas veces como sea el resultado del siguiente cálculo: l/d-1. Es decir, repetirá la línea 5 la cantidad de pares de palos pequeños que pueda haber en un palo largo, le restaremos uno para que no cuente el palo del final. Para evitar confusiones, lo truncaremos, usando la función int(), que trunca cualquier número.
-
Añade a la lista del paso 1 la posición de cada par de palos pequeños. Como bien hemos dicho antes, esta acción se repetirá tantas veces como pares entren. El cálculo que hace es d*(i+1). i es un contador que pertenece a la función for i in range () de la línea 4. Esta función lo que hace es repetir lo que viene debajo (en este caso la línea 5) mientras i sea menos que el número entre paréntesis. Al ser i parte de una función de Python, se actualiza solo al acabar cada repetición, pero también empieza en 0, no en 1. Por lo que, a i le sumaremos 1 para poder multiplicarlo correctamente. Si no, la primera vez sería 0, ya que d·i = d·0 = 0.
-
Crea una variable llamada pPalo, que hace referencia a la cantidad de palos pequeños que entren en cada palo largo. La cantidad de la variable será la longitud de la lista p*2. Recordemos que la lista p hace referencia a las posiciones de cada par de palos pequeños en cada palo largo, de forma que la longitud de la lista será el número de pares totales. Así que solo falta multiplicarlo por 2 para saber el total en vez de cada par.
-
PARTE OPCIONAL. Repite el programa de las líneas 8 y 9 tantas veces como el resultado de pPalo/2 sea. Es decir, lo que hace es repetir el programa tantas veces como pares haya.
-
PARTE OPCIONAL. Aplicamos un condicional, el famoso “if”. En el caso de que el elemento i de la lista p (posición de los pares) sea un número entero, sucederá la línea 9, si no, la omitirá. Cabe recordad que i varía en cada repetición, ya que forma parte de la instrucción “for i in range ()”. IMPORTANTE: al recoger al principio los datos de las dos variables con tipo “float”, se añaden decimales que a veces son innecesarios, como por ejemplo el de 2.0 o 1.0… Siguen siendo enteros, pero con decimales.
-
PARTE OPCIONAL. Transformará el elemento i de la lista p (posición de los pares) en un entero sin decimales, para hacer más bonita su representación posteriormente.
-
Escribe “Número de palos pequeños por cada palo largo: ” seguido del número de palos pequeños por cada palo largo, la variable pPalo.
-
Escribe “Posiciones de los palos pequeños en cada palo largo: ” seguido de las posiciones de los palos pequeños en cada palo largo, la lista p.
-
Escribe “Número de palos pequeños totales: ” seguido de la multiplicación de pPalo (cantidad de palos pequeños en cada palo largo) * 6 (palos largos).
Representación interactiva en Geogebra del copo de nieve
En este applet de Geogebra puedes modificar los parámetros anteriormente comentados, y, con ellos, el copo de nieve.

Elaboración del copo en Geogebra
Paso de preparación
Primero vamos a hacer las variables, dos deslizadores: uno de “Longitud” y otro de “Distancia”. Aconsejo máx. 10 y 5 respectivamente.
Paso 1
Para elaborar el copo, tienes que partir de un hexágono (copo de 6 palos). Una forma de hacer el hexágono, es haciéndolo inscrito en una circunferencia. Para ello, deberás hacer una circunferencia con radio n y centro en A. A un extremo del diámetro lo llamaremos B y al otro, C. Ahora, haremos una circunferencia con centro en B y radio r (el mismo que antes) y otra circunferencia con centro en C y radio r (el mismo que las otras dos veces).
Paso 2
Después de dibujar estas dos circunferencias, tenemos cuatro puntos de intersección de estas circunferencias en la circunferencia principal. Marcaremos estos puntos y ocultaremos todas las circunferencias.
Paso 3
Haremos unos segmentos basados en su longitud. Hacemos 6, uno para cada punto, su punto de partida de todos será A, y su longitud la variable “Longitud”, solo faltará orientarlos de forma que pasen por los puntos del paso 2.
Paso 4
A continuación haremos tantas circunferencias como el máximo del deslizador de “Longitud” sea. Todas tendrán centro en A, y su radio será progresivo, es decir: la primera, radio = Distancia·1; la segunda, radio = Distancia·2… Así tantas veces como el máximo del deslizador “Longitud” sea.
Paso 5
Ponemos el deslizador de “Longitud” al máximo y el de “Distancia” al mínimo, esto sería para simular el máximo de palos pequeños que se puedan representar. Ahora, tendremos muchos puntos de intersección entre estas circunferencias y los segmentos del paso 3. Marcaremos todos estos puntos y ocultaremos todas las circunferencias.
Paso 6
Si nos damos cuenta, si disminuimos el deslizador de “Longitud” o aumentamos el de “Distancia”, los puntos que no entran en los segmentos del paso 2, se ocultarán automáticamente. Ahora, con los deslizadores igual que el paso 5, haremos ángulos basados en su amplitud de todos los puntos, empezando por el final. Tal que así:
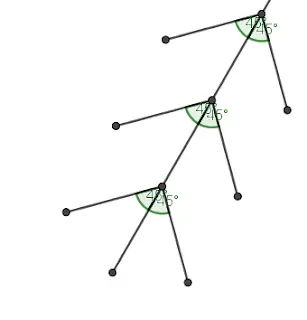
Paso 7
Ocultar todo y dejar solo los palos (largos y pequeños). De forma que ocultemos todos los puntos, todas las circunferencias y todos los ángulos. Ahora ya tendremos nuestro resultado final.

Paso extra
Dale color a tu copo de nieve y súbelo a la web de Geogebra para poder compartirlo, si vas a hacerlo, recuerda ocultar la barra lateral de “Vista algebraica”.
Aunque no lo parezca, hay muchas matemáticas en un pequeño copo de nieve. ¿Y tú? ¿Te has atrevido a hacer el copo de nieve en Geogebra?


